To solve quadratic equations using the quadratic formula, the given quadratic equation must be in the form of
ax2 + bx + c = 0
We can substitute the values of a, b, and c into the formula shown below and solve the quadratic equation given.
Example 1 :
Solve the quadratic equation using quadratic formula :
x2 – 5x – 24 = 0
Solution :
The given quadratic equation is in the form of
ax2 + bx + c = 0
Comparing
x2 – 5x – 24 = 0
and
ax2 + bx + c = 0
we get
a = 1, b = -5 and c = -24
Substitute the above values of a, b and c into the quadratic formula.
Therefore, the solution is
{-3, 8}
Example 2 :
Solve the quadratic equation using quadratic formula :
x2 – 7x + 12 = 0
Solution :
The given quadratic equation is in the form of
ax2 + bx + c = 0
Comparing
x2 – 7x + 12 = 0
and
ax2 + bx + c = 0
we get
a = 1, b = -7 and c = 12
Substitute the above values of a, b and c into the quadratic formula.
Therefore, the solution is
{3, 4}
Example 3 :
Solve the quadratic equation using quadratic formula :
15x2 – 11x + 2 = 0
Solution :
The given quadratic equation is in the form of
ax2 + bx + c = 0
Comparing
15x2 – 11x + 2 = 0
and
ax2 + bx + c = 0
we get
a = 15, b = -11 and c = 2
Substitute the above values of a, b and c into the quadratic formula.
Therefore, the solution is
{2/5, 1/3}
Example 4 :
Solve the quadratic equation using quadratic formula :
x + 1/x = 2½
Solution :
Write the given quadratic equation in the form :
ax2 + bx + c = 0
Then,
x + 1/x = 2½
x2/x + 1/x = 5/2
(x2 + 1)/x = 5/2
2(x2 + 1) = 5x
2x2 + 2 = 5x
2x2 - 5x + 2 = 0
Comparing
2x2 - 5x + 2 = 0
and
ax2 + bx + c = 0
we get
a = 2, b = -5 and c = 2
Substitute the above values of a, b and c into the quadratic formula.
Therefore, the solution is
{1/2, 2}
Example 5 :
Solve the quadratic equation using quadratic formula :
(x + 3)2 - 81 = 0
Solution :
Write the given quadratic equation in the form :
ax2 + bx + c = 0
Then,
(x + 3)2 - 81 = 0
(x + 3)(x + 3) - 81 = 0
x2 + 3x + 3x + 9 - 81 = 0
x2 + 6x - 72 = 0
Comparing
x2 + 6x - 72 = 0
and
ax2 + bx + c = 0
we get
a = 1, b = 6 and c = -72
Substitute the above values of a, b and c into the quadratic formula.
Therefore, the solution is
{-12, 6}

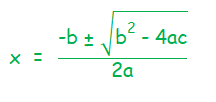
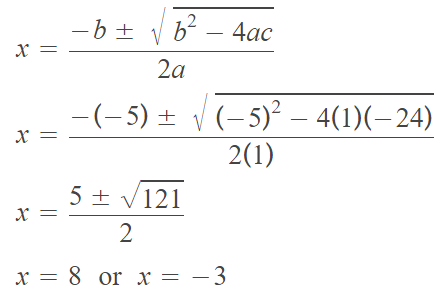
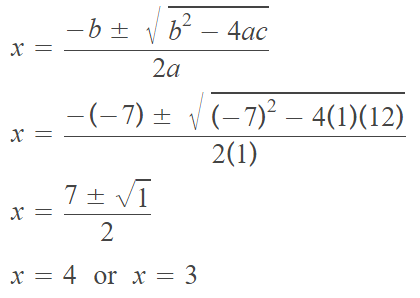
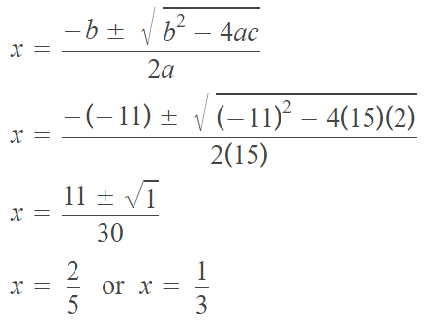
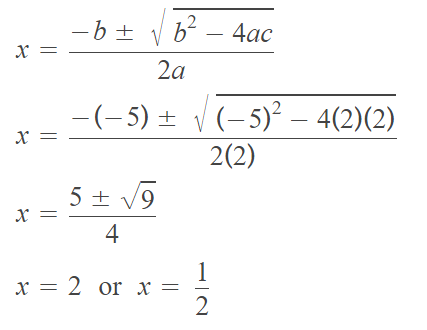
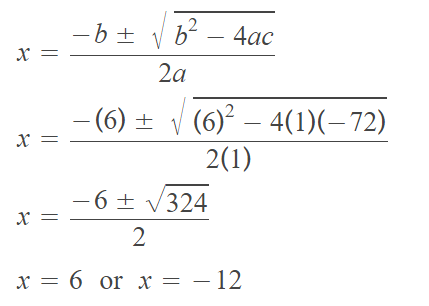



Comments
Post a Comment