EXERCISE 4.1 METRIC MATH

 

A polynomial looks like this:

example of a polynomial this one has 3 terms

Polynomial comes from poly- (meaning "many") and -nomial (in this case meaning "term") ... so it says "many terms"

A polynomial can have:

constants (like 3, −20, or ½)

variables (like x and y)

exponents (like the 2 in y2), but only 0, 1, 2, 3, ... etc are allowed

that can be combined using addition, subtraction, multiplication and division ...

... except ...

... not division by a variable (so something like 2/x is right out)

So:

A polynomial can have constants, variables and exponents,
but never division by a variable.

Also they can have one or more terms, but not an infinite number of terms.

Polynomial or Not?

These are polynomials:

3x
x − 2
−6y² − (79)x
3xyz + 3xy²z − 0.1xz − 200y + 0.5
512v⁵ + 99w⁵
5

(Yes, "5" is a polynomial, one term is allowed, and it can be just a constant!)

 

These are not polynomials

• 3xy^-2 is not, because the exponent is "-2" (exponents can only be 0,1,2,...)
• 2/(x+2) is not, because dividing by a variable is not allowed
• 1/x is not either
• √x is not, because the exponent is "½" (see fractional exponents)

 

But these are allowed:

• x/2 is allowed, because you can divide by a constant
• also 3x/8 for the same reason
• √2 is allowed, because it is a constant (= 1.4142...etc)

Monomial, Binomial, Trinomial

There are special names for polynomials with 1, 2 or 3 terms:

How do you remember the names? Think cycles!

There is also quadrinomial (4 terms) and quintinomial (5 terms),
but those names are not often used.

Variables

Polynomials can have no variable at all

Example: 21 is a polynomial. It has just one term, which is a constant.

Or one variable

Example: x⁴ − 2x² + x   has three terms, but only one variable (x)

Or two or more variables

Example: xy⁴ − 5x²z   has two terms, and three variables (x, y and z)

What is Special About Polynomials?

Because of the strict definition, polynomials are easy to work with.

For example we know that:

• If you add polynomials you get a polynomial
• If you multiply polynomials you get a polynomial

So you can do lots of additions and multiplications, and still have a polynomial as the result.

Also, polynomials of one variable are easy to graph, as they have smooth and continuous lines.

Example: x⁴−2x²+x

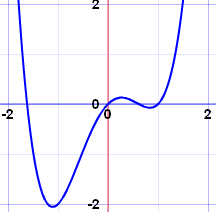See how nice and smooth the curve is?

You can also divide polynomials (but the result may not be a polynomial).

Degree

The degree of a polynomial with only one variable is the largest exponent of that variable.

Example:

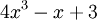The Degree is 3 (the largest exponent of x)

ایک متعدد شکل کچھ اس طرح دکھائی دیتی ہے۔

متعدد مثال

متعدد کی مثال

اس کی 3 شرائط ہیں

متعدد کثیرالجہتی (جس کا مطلب "بہت سارے") اور اسمانی (اس معاملے میں معنی "اصطلاح") سے آتا ہے ... لہذا اس میں "بہت سی شرائط" کہا جاتا ہے

ایک متعدد ہوسکتا ہے:

مستقل (جیسے 3 ، −20 ، یا ½)

متغیر (جیسے x اور y)

اخراج (جیسے y2 میں 2) ، لیکن صرف 0 ، 1 ، 2 ، 3 ، ... وغیرہ کی اجازت ہے

جو اضافہ ، گھٹاؤ ، ضرب اور تقسیم کا استعمال کرتے ہوئے جوڑ سکتا ہے ...

... سوائے ...

... متغیر کے لحاظ سے تقسیم نہیں (لہذا 2 / x جیسا کچھ ٹھیک ہے)

تو:

کثیرالقاعدی میں مستقل ، متغیر اور اخراج کرنے والے افراد ہوسکتے ہیں۔

لیکن کبھی بھی متغیر کے حساب سے تقسیم نہیں ہوتا ہے۔

نیز ان کی ایک یا زیادہ شرائط ہوسکتی ہیں ، لیکن اصطلاحات کی لامحدود تعداد میں نہیں۔

متعدد یا نہیں؟

متعدد

یہ متعدد ہیں:

3x

x - 2

y6y2 - (79) x

3xyz + 3xy2z - 0.1xz - 200y + 0.5

512v5 + 99w5

5

(ہاں ، "5" متعدد ہے ، ایک اصطلاح کی اجازت ہے ، اور یہ محض ایک مستقل ہوسکتا ہے!)

 

یہ متعدد نہیں ہیں

3 آکسی 2 نہیں ہے ، کیونکہ ضائع کرنے والا "-2" ہے (خاکہ صرف 0،1،2 ہوسکتا ہے ، ...)

2 / (x + 2) نہیں ہے ، کیونکہ متغیر کے ذریعہ تقسیم کی اجازت نہیں ہے

1 / x بھی نہیں ہے

√x نہیں ہے ، کیونکہ ضائع کرنے والا "is" ہے (جزوی خاکہ دیکھیں)

 

لیکن ان کی اجازت ہے:

x / 2 کی اجازت ہے ، کیونکہ آپ مستقل طور پر تقسیم کرسکتے ہیں

اسی وجہ سے 3x / 8 بھی

√2 کی اجازت ہے ، کیونکہ یہ مستقل ہے (= 1.4142 ... وغیرہ)

Monomial ، Binomial ، Trinomial

1 ، 2 یا 3 شرائط کے ساتھ متعدد ناموں کے خاص نام ہیں۔

منیومئیل ، بایومینیئل ، تثلیاتی

آپ کو نام کیسے یاد ہیں؟ سوچو سائیکل!

مونوسیکل سائیکل ٹرائی سائیکل

یہاں چوکور (4 اصطلاحات) اور کوئنٹومیومیل (5 اصطلاحات) بھی ہیں ،

لیکن وہ نام اکثر استعمال نہیں ہوتے ہیں۔

متغیرات

کثیر الجماعی میں کوئی تغیر نہیں ہوسکتا ہے

مثال: 21 ایک متعدد ہے۔ اس کی صرف ایک اصطلاح ہے ، جو مستقل ہے۔

یا ایک متغیر

مثال کے طور پر: x4 - 2x2 + x کی تین اصطلاحات ہیں ، لیکن صرف ایک متغیر (x)

یا دو یا زیادہ متغیرات

مثال کے طور پر: xy4 - 5x2z کی دو شرائط ہیں ، اور تین متغیر (x ، y اور z)

کثیر الجماعی کے بارے میں کیا خاص بات ہے؟

سخت تعریف کی وجہ سے ، کثیرالعمل کام کرنا آسان ہیں۔

مثال کے طور پر ہم جانتے ہیں کہ:

اگر آپ کثیرالقاعدہ شامل کرتے ہیں تو آپ کو کثیر الجماعی ملتا ہے

اگر آپ کثیر الجماعی کو ضرب دیتے ہیں تو آپ کو کثیر الجماعی ملتا ہے

لہذا آپ بہت سارے اضافے اور ضربیں کرسکتے ہیں ، اور اس کے نتیجے میں ایک کثیرالجہتی ہے۔

نیز ، ایک متغیر کے کثیر الجماعات گراف میں آسان ہیں ، کیونکہ ان کی ہموار اور مستقل لائنیں ہوتی ہیں۔

مثال کے طور پر: x4−2x2 + x

x ^ 4-2x ^ 2 + x

دیکھو کتنا اچھا اور

ہموار ہے؟

آپ کثیرالقادیات کو بھی تقسیم کرسکتے ہیں (لیکن نتیجہ متعدد نہیں ہوسکتا ہے)۔

ڈگری

ایک متغیر کے ساتھ متعدد کی ڈگری اس متغیر کا سب سے بڑا اخراج ہے۔

مثال:

4x3-x-3 ڈگری 3 ہے (ایکس کا سب سے بڑا اخراج کنندہ)